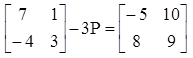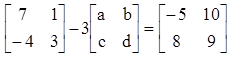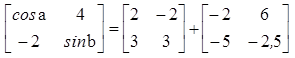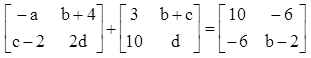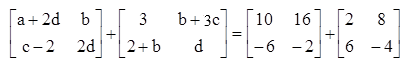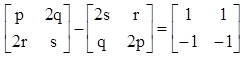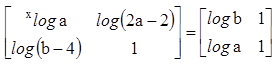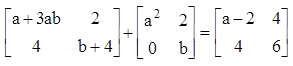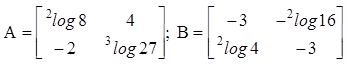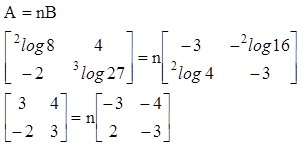Soal Dan Pembahasan Kesamaan Matriks

Dua atau lebih matriks dibilang sama bila memiliki ordo (jumlah baris dan kolom) sama dan unsur yang serupa di setiap selnya. Dengan kata lain , matriks-matriks tersebut merupakan matriks yang serupa cuma saja dengan nama berbeda.

Prinsip kesamaan matriks kebanyakan digunakan untuk menyeleksi unsur pada sel tertentu atau menyeleksi variabel yang terdapat dalam unsur penyusun matriks.

Prinsip kesamaan matriks biasanya dihubungkan dengan persamaan matematika yang lain seumpama persamaan linear dua variabel , persamaan kuadrat , eksponensial , logaritma , ataupun trigonometri.

Konsep Kesamaan Matriks

Bila dua matriks di atas dinyatakan sama , maka berlaku :
a = p; b = q; c = r
d = s; e = t; f = u
g = v; h = w; l = x

Kumpulan Soal

Jika dipahami matriks A dan B seumpama di bawah ini , maka tentukanlah hubungan antara B + A dan A + B.

Pembahasan :
Sudah sungguh terperinci bahwa pada operasi penjumlahan matriks berlaku sifat komutatif sehingga B + A = A + B.
Sebuah matriks P ordo 2 x 2 menyanggupi persamaan seumpama di bawah ini , tentukanlah matriks P.

Pembahasan :
Misalkan elemen-elemen matriks P merupakan a , b , c , dan d

7 – 3a = -5 —> -3a = -12 —> a = 4
1 – 3b = 10 —> -3b = 9 —> b = -3
-4 – 3c = 8 —> -3c = 12 —> c = -4
3 – 3d = 9 —> -3d = 6 —> d = -2
Jadi matriks P merupakan :
Tentukanlah nilai x dan z yang menyanggupi persamaan matriks berikut ini :

Pembahasan :
-1 + 6 = 2 + 2x
5 = 2 + 2x
3 = 2x
x = 3/2
3 + 2 = 3 + z + 1
5 = 4 + z
z = 1
Tentukan besar sudut a dan sudut b.

Pembahasan :
cos a = 2 + (-2) = 0 —> a = 90
sin b = 3 + (2 ,5) = 0 ,5 = 1/2 —> b = 30
Diketahui persamaan matriks selaku berikut :

Tentukanlah nilai a , b , c , dan d.
Pembahasan :
-a + 3 = 10 —> a = -7
c – 2 + 10 = -6
c = – 6 – 8
c = -14
b + 4 + b + c = -6
2b + c = -10
2b – 14 = -10
2b = 4
b = 2
2d + d = b – 2
3d = 2 – 2
d = 0
Berdasarkan persamaan matriks di bawah ini , tentukanlah nilai a , b , c , dan d.

Pembahasan :
2d + d = -2 + (-4)
3d = -6
d = -2
a + 2d + 3 = 10 + 2
a + 2(-2) = 12 – 3
a – 4 = 9
a = 9 + 4
a = 13
b + b + 3c = 16 + 8
2b + 3c = 24
c – 2 + 2 + b = -6 + 6
c + b = 0 —> c = -b —> substitusi ke persamaan 2b + 3c = 24
2b + 3(-b) = 24
2b – 3b = 24
-b = 24
b = -24 maka c = 24
Jadi a = 13. b = -24 , c = 24 , dan d = -2
Jika p , q , r , dan s menyanggupi persamaan matriks

Pembahasan :

Dari soal , diperoleh 4 persamaan yakni :
1. p – 2s = 1
2. 2q – r = 1
3. 2r – q = -1
4. s – 2p = -1
Dari persamaan no 1 dan 4 diperoleh :
p – 2s = 1 —> p = 1 + 2s —> substitusikan ke persamaan 4
s – 2p = -1
s – 2(1 + 2s) = -1
s – 2 – 4s = -1
-3s = 1
s = -1/3
selanjutnya ,
p – 2(-1/3) = 1
p + 2/3 = 1
p = 1 – 2/3 = 1/3
Dari persamaan no 2 dan 3 diperoleh :
2q – r = 1 —> -r = 1 – 2q —> r = 2q + 1 —> substitusi ke persamaan 3
2r – q = -1
2(2q + 1) – q = -1
4q + 2 – q = -1
3q = -3
q = -1
selanjutnya ,
2(-1) – r = 1
-r = 1 + 2 = 3
r = -3
Jadi p = 1/3 , q = -1 , r = -3 , dan s = -1/3
Tentukan nilai x yang menyanggupi persamaan matriks di bawah ini.

Pembahasan :
Dari hubungan di atas , diperoleh
log (2a – 2) = 1
log (2a – 2) = log 10
2a – 2 = 10
a = 12/2 = 6
log (b-4) = log a
log (b-4) = log 6
b-4 = 6
b = 10
^xlog a = log b
^xlog 6 = log 10
^xlog 6 = 1
x = 6
Jadi nilai x yang menyanggupi persamaan di atas merupakan 6
Tentukan nilai a

Pembahasan :
a + 3ab + a² = a – 2
a – a + 3ab + a² + 2 = 0
a² + 3ab + 2 = 0 —> persamaan kuadrat
Agar persamaan di atas sanggup teratasi , kita cari nilai b apalagi dahulu.
b + 4 + b = 6
2b = 6 – 4
b = 2/2 = 1
Persamaan kuadrat di atas menjadi :
a² + 3a + 2 = 0
(a + 2) (a + 1) = 0
a = -2 atau a = -1
Tentukan hubungan matriks A dan B jikalau dipahami

Pembahasan :
Karena soal ini tergolong pada belahan kesamaan matriks , maka anggaplah bahwa A = nB , dengan n merupakan sebuah bilangan tertentu yang menerangkan hubungan keduanya.

Dari hubungan di atas , biar bernilai sama maka nilai n = -1
maka A = -B